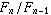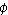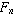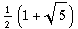MATHEMATICS
Numbers, Quantities, Values and Geometry
March 2006  - latest update January 15th 2010

Why am I writing this? Because so many mathematicians appear to be unable to experience the typical difficulties that those who consider themselves non-mathematicians have in relating the language of maths beyond simple addition, subtraction, multiplication and division, to the world of their experience. Because they are mathematically adept they are usually suitable teachers only for the similarly gifted. Because they can successfully manipulate and manoeuvre in the mathematical medium, they can also gloss over some of the anomalies. "Don't worry about that, it just works", they will say. But a non-mathematician may think: "hold on, that's a nice box of meccano but its a human convention - and yet when you are asked to explain it, there are things that can't be explained by humans. Maybe there is a flaw in your maths."

If you can read and fully appreciate all this: http://en.wikipedia.org/wiki/Euler%27s_identity  - then you may not need to read the rest of my file, but you may not be a very good maths teacher either.

So, here we are going to take another look at some of our mathematics, and see if we can remove some artificial mysteries and change some people's frustration to happiness. I will start with NUMBERS, but right away I must point out that the world is experienced through what we call geometry, which includes numbers not only as the way of agreeing to ourselves and with others that existence is plural, but that this plurality exhibits qualities and quantities in a way that would demand an almost infinite combination and arrangement of numbers if we were to reduce it to a formula on a piece of paper. Yet this is exactly what we have demanded of mathematics in the last few centuries to do.

We now ask it to describe, in numbers and symbols on a flat sheet of paper without a single drawing, let alone a model, any object or process we have known or can imagine. Now we also ask these numbers and symbols to show what it will do over time, in a dynamic situation. And because we cannot wait for or pay someone to reproduce, or build anew every time, the reality it describes, and because we cannot as non-geniuses read the mathematics like a great musician reads a musical score, thereby experiencing it in our minds, we get the mathematics written in code and embedded in a laser or magnetic disc or electronic memory that releases it at an unimaginable speed into a device that will play it for us in pictures and in sound, in a simulation of the real world or another. If we like what it plays, we can get the output sent to a machines which will seek and mix and mould and extrude and carve and convert the designs of the math into objects, and these objects may be machines that enable this very process to advance to a higher level...

We call geometry written without the use of drawings or models, algebra. Although both geometry and forms of algebra existed independently in some contexts long before him, his day it was Rene Descartes who first established the formal, orthodox relationship between the two. [Note: We do not need to go back just here to the Greeks and Persians, Indians, Arabs and others who shaped the building blocks of mathematics, suffice to say it took all of them together and a later assembly job by people we now think of as 'western', to bring into being the system of mathematics as used today. It is a truly global product. It should be appreciated that these 'Western' societies were formed themselves with a mix from the former]

So when we start with numbers, we should understand that some of the conventions we use are based on requirements long ago that were very much more basic than those which we require of these numbers today. One of the conventions that gives us some trouble now is the one for the simple signs + (plus) and - (minus). Bear with me. I would shorten this if I could, but I need to cover the ground. In the world of our experience, the 'real world', the minus sign can be used, when we have a quantity, to denote less of that quantity. If we have ten camels, and we take 4 away, how many are there? The answer is there are still 10, but 4 of them are now elsewhere. You can only take something away if there is a place it can be taken to. If you kill one camel, you have 9 live camels and one dead camel. If you could cut that camel into bits you would have 9 camels and a greater number than 1 of camel bits. If the camel is eaten by predators, it can then over time be said to have been converted into an ever increasing number of pieces of differently identifiable matter and in due course some radiant energy. You then truly only have nine camels plus a lot of stuff you may not be able to lay your hands on (or want to). But you cannot have minus one camels.

You cannot have a real overdraft. If you spend money you do not have, you have spent your bank's money. They will want it back and you will have to get some off someone else (an employer, a friend, the government, another bank, a dividend or a sale for example) to pay them back, meantime they they will charge you interest. Because we work with symbolic (virtual) money these days, those who control the money supply can of course create money, but they have to be careful as the lesson of a particular type of inflation caused by printing credit or banknotes not justified by a contribution to the global wealth on a par with other comparable national banks and related to individual and communal effort, has been learned. [Note: Even if the world's nations expand the money supply in a coordinated way they must be careful to make it a correction after a bust bubble, to match reality, otherwise people will bid up the price of gold because a quantitative easing of gold has real costs in labour. It cannot be printed on paper or shown on a electronic statement. Why gold? Another time, not now please!]

So a negative number on a balance sheet or a bank account denotes, just like our story of the camels, that this money is in another place. Your bank account shows minus £10, the shop where you have just spent the money adds +£10 to its float. If the shop owes its bank £1,000, there is a -£1,000 written somewhere and a +£1,000 written in another column which is a good, not a bad debt and therefore an asset. If the shop goes bust and the bank writes off the debt, the + £1,000 and the -£1,000 disappear simultaneously. You cannot have minus £1,000.

However, we can have minus numbers, as we see from the above, and numbers can refer to more than real existence or virtual existence. A number will refer to a VALUE, and that value can be more than the answer to the basic question - to be or not to be. It can be one of the other values that came up in the story of the camels, answering the questions WHERE and WHEN. When did we take 4 camels away and where did we put them? Before we can have more than one thing we have to have places for them to be and time for them to be there. We have to have Space-Time, in other words what we call DIMENSIONS. If we are to take 4 camels away in one direction, it will certainly be describable with some degree of accuracy by a values in two dimensions. Imagine we take 2 camels 10 miles in one direction and another another two 5 miles in the opposite direction. If we are to describe the position of the camels on the line that joins them, we can take the original site as ground zero and call the other localities +10 and -5. Of course these values could all be positive if we imagined some absolute ground zero miles away and put the original site at a value relative to that absolute, but this is immensely impractical! So we mathematically denote values along the North-South line as positive in one direction and negative in the opposite one. We do that to avoid having more than one 'ground zero', and also to mark any landmarks, relative to the scenario at hand.

Now of course we have, in the real world, lots of things that are not on that line at all, so a second dimension is recognised immediately in the mathematics of our situation. Let us take a line at right angles to the first. This has values that are not even contained in the first dimension. Now let us imagine swinging this second line clockwise and anti-clockwise. If we use numbers for the degrees of rotation and we use positive numbers for clockwise degrees, then anticlockwise swings would use negative numbers to give the value.

Why am I talking about this? In order to explain that the numbers that were first used to count existing objects, and to which we applied the convention of positive and negative and equated these with plus and minus, must unfortunately lose some of the meanings of MINUS when they do not refer to EXISTENCE but to purely calculational or abstract or directional VALUE. In the arithmetic of existence, -5 x -5 makes +25. But if that minus sign means a direction or a directional component of a velocity, then two negatives multiplied do not always make a plus.

That in  nutshell is why we can have the square root of minus one. It is needed, if for no other reason (though there are important others), as the square root of a value of one, in a direction opposed, in the context of any formula, to equivalent positive values. These values could be in time as well as in space, they can refer to charge or spin and to measurements in any one of the 4 dimensions without negating, even when influencing, the others. So there is no mystery about it at all, there is just a confusion about the meaning of + and - caused by our assumption that we could use these to describe opposition in totality and at the same time opposition in specific single geometric dimensions or values. On a graph where '+' is marked to the right of a vertical line and ' - ' to the left of that vertical, zero lies on the vertical line, half way between -1 and +1. The square root of minus one on that graph lies just as far to the left of zero as the square root of plus one lies to the right of it. It is only if we call it -1 and then say -1 times -1 equals plus one, because it does in simple arithmetic and simple algebra, that we are in trouble.

Because mathematicians persist with using the symbols + and - and the concepts associated with both, the orthodox discussion on this subject and the use of the + and - symbols in this context has become absolutely incomprehensible to ordinary mortals. William Rowan Hamilton had some sensible ideas to update the conventions but I am not sure anyone took him up on it. As far as this dissertation is concerned we have covered the reason for and the reality of the square root of minus one and for that matter any other minus number and we shall move on.

Next: Why are there so many recurring numbers in the decimal system?
Answer: Because early man used his thumbs as part of the digital counting system instead of as the pointer or reader of other fingers on the same hand, as he should have done and could have done.

A system based on Twelve would have been OK, one based on Eight  would have been good. One based on ten was a bummer. You will note I write them in words, not in digits (note: the word digit = finger). If early man had used his thumb to count on his fingers instead of his other hand (which should have been busy picking things up or holding them) we would have had at least an octal system.

In a dodecimal (Twelve base) system we would count 1,2,3,4,5,6,7,8,9,X,Y,10,11,12,13,14,15,16,17,18,19,1X.1Y,20
Of course we would have two unique new symbols and words, not Y and Y as I have written.

Then X (which we currently write as 10) could be divided by 3 and give an answer as follows:
3 into X goes 3 and 1 over, 3 into new 10 (which equals 12 in old decimals) goes 4, so the answer is 1.4  - note that is not a decimal point, it is a dodecimal point!!

Base 8 gives us 1,2,3,4,5,6,7,8,10,11,12,13,14,15,16,17,18,20,21,22,23,24,25,26,27,28,30

3 into 4 goes 1 and 1 over, 3 into new 10 (old 9) goes 3, answer 1.3  (that is an octal point)
3 into 5 goes 1 and 2 over,  3 into 20 goes 6, answer 1.6

Whereas in the decimal system, if we divide the 10th number by 3 we get 3.33333333 recurring for ever.

There are many fractions that give recurring numbers in the decimal system just because so many numbers don't divide handily into a counting system based on our total number of fingers and thumbs, but these must not be confused with numbers that do not resolve to a finite number of digits for other reasons. I will deal with pi ( π ) just to give you the idea.
 π.is a number we write as the Greek letter P in lowercase, pronounced pie and also written pi. It relates the diameter of a circle to its circumference
π is classed as both irrational and transcendental.

It has been calculated to be 3.141592653589793238462643383279502884197......... etc, never repeating or ending.

Formulae for pi are at http://mathworld.wolfram.com/PiFormulas.html

Here is a conventional explanation of irrational and transcendental numbers. You are not going to like it if you are not a mathematician:

An irrational number is a number that cannot be expressed as a fraction p/q for any integers p and q. Irrational numbers have decimal expansions that neither terminate nor become periodic. Every transcendental number is irrational.
A transcendental number is a number that is not the root of any integer polynomial, meaning that it is not an algebraic number of any degree. This definition guarantees that every transcendental number must also be irrational, since a rational number is, by definition, an algebraic number of degree one. A number x can then be tested to see if it is transcendental using the Mathematica command Not[Element[x, Algebraics]].

I have lifted the above 2 paragraphs from MathWorld, and if you click the links you can get more of that, but now I am just going to give you a very simple explanation of why π can never come out as an exact fraction or finite decimal. It is very, very simple. π is the ratio of the diameter of a circle to its circumference.   π x D is the length of the curved line that describes the circle of diameter D. We can describe the length D in any unit we like. Let us say centimetres for example. Now a centimetre is a straight line measurement. We only have straight line units of length. Of course in practice we can take a wire of a certain length and wind it round a curve, but we are looking here for extreme accuracy based on theory, not practice. We are looking for accuracy of the level of, for example, 4/2 = 2, geddit? Not nearly 2, not very nearly 2 to a million places of decimals, but exactly. So you can see that to get an exact answer for π,.we would have to have our circumference measured in straight line units infinitely smaller than straight line centimetres we chose for our straight line diameter, so that the error caused by averaging the theoretical measuring units constructed tangentially on the outside and those constructed as an internal regular polygon was reduced to zero. We could go on making these units smaller and smaller for ever in theory. So in theory there is no limit to the accuracy to which we could measure π - because we are measuring a curve with straight line units. In practice there is a limit, as the physical world, while analogue in macro practice, is digital in atomic practice; so an actual circle, rather than a theoretical circle, is made up of atoms with a limit below which curvature is no longer real. But theoretical π cannot reach the end.

It is not possible to square the circle, we are told, meaning it is not possible to find in practice either, using a ruler and compass, to find or construct a square with exactly the same area as a circle. just as with the theoretical (these days computerised) construction of internal and external polygons, the work with ruler and compass would go on an on getting nearer but never arrive at an end or even an approximation that was legible! But there is something more fascinating though simpler and maybe even more significant about π  and that is not what it is, but what it isn't!   It is NOT 3.

It is possible to imagine a disk on the surface of a sphere for which the ratio of the diameter to the circumference would be exactly 3. Perhaps some reader would care to work out what the ratio of the diameter and circumference of the disk would have to the diameter and circumference of the sphere it is inscribed on to arrive at this pi=3 property. It must be a constant. It will either have a relationship to a known existing constant or be a new one. To discover a new constant would be quite something, so I imagine it is derivative of the existing one. The non-threeness of pi represents the dimensional tensioning of space-time in its dynamic existence. It is the tension of the in bowstring of creation of the string on which is played the music of the spheres. Terry Pratchett imagines, I am told, in Going Postal, a place where a wheel has a value for pi that is exactly 3. This triggers a chain of events that leads to to the destruction of the universe. I have not read the book, but I think it most certainly would! The material universe depends for its existence on this dynamic dimensional tension.

THE GOLDEN RATIO and FIBONACCI NUMBERS
There are some numbers and proportions that occur in nature. I call again on MathWorld to kick off:

The Fibonacci numbers give the number of pairs of rabbits n months after a single pair begins breeding (and newly born bunnies are assumed to begin breeding when they are two months old), as first described by Leonardo of Pisa (also known as Fibonacci ) in his book Liber Abaci. Kepler  also described the Fibonacci numbers (Kepler 1966; Wells 1986, pp. 61-62 and 65). Before Fibonacci wrote his work, the Fibonacci numbers had already been discussed by Indian scholars such as Gopala (before 1135) and Hemachandra (c. 1150) who had long been interested in rhythmic patterns that are formed from one-beat and two-beat notes or syllables. The number of such rhythms having n beats altogether is Fn+1, and hence these scholars both mentioned the numbers 1, 2, 3, 5, 8, 13, 21, ... explicitly (Knuth 1997, p. 80).


The ratios of successive Fibonacci numbers fibrat approaches the golden ratio phi as n approaches infinity, as first proved by Scottish mathematician Robert Simson in 1753 (Wells 1986, p. 62). The ratios of alternate Fibonacci numbers are given by the convergents to phi, where Fn is the golden ratio, and are said to measure the fraction of a turn between successive leaves on the stalk of a plant (phyllotaxis): 1/2 for elm and linden, 1/3 for beech and hazel, 2/5 for oak and apple, 3/8 for poplar and rose, 5/13 for willow and almond, etc. (Coxeter 1969, Ball and Coxeter 1987). The Fibonacci numbers are sometimes called pine cone numbers (Pappas 1989, p. 224). The role of the Fibonacci numbers in botany is sometimes called Ludwig's law (Szymkiewicz 1928; Wells 1986, p. 66; Steinhaus 1999, p. 299).
.

IN SIMPLE LANGUAGE
The Fibonacci series is formed by creating the next number from the sum of the last two. As it says in the preceding paragraph, the ratio of successive Fibonacci numbers approaches the GOLDEN RATIO as the number advances.
In our math, The Golden Ratio is Phifract which is  1.618033988749894848204586834365638117720....  in decimal, written as Greek PHI
In this case we cannot justify the endless number on the grounds of relating straight line units to curved measurements, even if we could justify it as artificially endless in decimal linear arithmetic. It is another story. The Golden Ratio is based on one of the simplest proportions imaginable Don't be misled by the arbitrary appearance of the formula above of the number 5. That is indeed an ingenious formula for calculating the ratio; but the value itself is self creating, and that is why (I will argue below) it appears in nature. It is the ultimate proof of the principle of Natural Selection.
Golden Ratio 
In the line AB above, the ratio of length CB to AB is the same as the ratio AC to AB. There is nothing more basic or self contained than that. To find the point C on that line where this is true needs a bit of nifty but understandable geometry which we will look at later. But as soon as you have a real Space-Time, with energy-driven dynamic processes, this point will be found by resonance between the patterns of energy and matter that sense their mutual but separate existence.

It is a proportion that creates itself and, thereafter, will detect matching examples through resonance. It will tend to produce stability, with the possibility of adventurous harmonics. This would be inevitable as soon as energy emerges from a singularity and forms plurality.

It will therefore preponderate in any reality that is the result of mutual selection. Natural Selection is the universal form of mutual selection. The Golden Ratio's appearance in Nature is therefore inevitable on the basis of Natural Selection, which starts to show it's presence long before the formation of solar systems and life. By the time we get to plants and animals, proportions that tend toward the Golden Ratio will have set the standard for environmental compatibility. Fibonacci numbers will therefore be the default in nature, as, however numerically modest, they are always tending toward the ultimate Golden Ratio as they build.

There is therefore nothing mystical, strange, peculiar or illogical about the preponderance or significance of these numbers or ratios in nature. They are an inevitable consequence following from the emergence of dimensional space-time from the energy source.

MARCH 24th 2006
I have had few questions from interested readers. As usual I have to admit to (almost) never having read anything about the subjects I write about, the last time I learned anything about the Golden Ratio was with an architect cousin who told me about it's simplest form when I was 8 in 1946, so I have to go and find stuff half way through to back up my own thoughts. In this case I am pleased to say a Google search brought me this PHI: The Divine Ratio, so rather than stretch my brain any more here's someone who has done it already. This saves me an enormous amount of time as what I was going to speculate has already been studied and is known. I feel a bit of a twit in one way now as it goes further than I had thought, ecouraged in another. Mind you I am not into mysticism or the 'sacred'. Either the whole universe is sacred or nothing is, so the term has little meaning. As far as behaviour is concerned, that's something else. Murphy's law says 'anything that can go wrong will go wrong', and if parts of the universe could not go wrong they would not have freedom, and that would probably contradict the freedom for anything to come into being in the first place. As the material universe evolved it found sustainable arrangement through the alternatives of entropy or gravitationally induced mutual compatibility and aggregate complexity. Once we get to human life the level of autonomy and freedom is of a different order, but Murphy's law still applies, as does Ockham's.Razor I would guess. OK, look it up.

Having delved a bit further into the author of the web site I have linked in the previous paragraph  David Yarrow I find we have certain things in common, particularly a point in each of our lives when we worked out that a key to good health is food. He is, however, infinitely more accomplished than I am !

It is important before reading through the pages of David Yarrow's web site that deal with the 1st, 2nd, 3rd, 4th and 5th dimensions to get to grips with what he calls a simple pentagon. He does not tell you how to draw this, so here is my guess. The five sides between them turn through 360 degrees to return to the original side. 360/5 = 72 so each side is 72 degrees from the previous one. 180-72 = 108, so the internal angles of a pentagon are 108. A pentangle contructed as shown by Yarrow will have internal apex angles therfore of 180-144 = 36. No doubt there is way of drawing all this with just a compass and ruler, without a protractor but I haven't got the tools or figured it out yet.

MARCH 28th 2006
Today at 3.30 on BBC Radio 4, Robert Powell read: "Golden Mean, a moving tale of first love, mathematics, irrational numbers and the idea of eternity", written by Alan Garner. I would really like to put a link to it here, to the BBC Web Site, to a 'listen again' option. But mysteriously there is no mention of this programme or even of the series of 5 of which it is the second, called Lucky Numbers. Fortunately I have a copy of the Radio Times which tells me I was not dreaming... I thoroughly recommend this and hope it will be repeated. It contained more philosophy than math, but the philosophy was phine.

MARCH 29th
Another shape which tends to form and reproduce itself by natural selection is the Hexagon. It has some recursive but no transcendant or irrational properties. A single value, the radius of a circle, if drawn as a chord of the same circle and repeated contiguously within the circle will, after 5 repetitions, form a regular hexagon - the six-sided pattern known as honeycomb - which can be fitted together on a flat surface with other identical shapes leaving no wasted space. The combined length of these is logically exactly 3 times the diameter of the original circle, proving at a stroke that Pi must be just a bit more than 3. That 'bit' is difference in length between the 6 chords (equal to 3 diameters because we chose the radius as their length) and the 6 sectors of the circle that these chords define.

Let us now look at the Pentagon and Hexagon and the complete Pentagram and Hexagram which produce tthe Pentangle and Hexangle
Pentagon
 hexagon
pentagram
 hexagram
 
Points to note:The 72 degree angle of progression of the Pentagon shows up in the Pentagram which is drawn by joining alternate apexes of the Pentagon. It's periphery describes a Pentangle.  The only triangles are the 5 small isocelese ones, with base angles 72, leaving 36 degrees for the angle at each of the 5 points of the 'star'. As you follow the line from any apex till it reflects from the circumference, it covers the entire Pentagram before returning to the start. A smaller Pentagon is generated in the centre of the Pentagram. The sides of the angles which form the points of the star intersect the sides of next angle at proportions which give us the Golden Ratio, over and over again.

Now consider the Hexagon. I have filled in some inside equilateral triangles to show how it is constructed from angles of 60 degrees only and all lines of the same length, internally and externally. Moving down to the Hexagram contructed by joining (as we did with the Pentagon) alternate apexes (apices), we see there are six small equilateral triangles making the points of the Hexangle star, there is a new Hexagon generated in the centre, but if we follow the line from one apex as it reflects off the circumference it forms a large, closed equilateral triangle. Unlike the Pentangle the next apex is part of another large, distinct equilateral triangle. All angles are 60 degrees or their inevitable adjacent value of 120. All the values are rational and all the lengths are the same and can be whole numbers

BUT, both of these forms have a relationship with Pi, and the sum of the apex angles of the Pentangle add up to 180, those of the Hexangle to 360, so they are cousins in one way though strangers in another. This difference makes their combination adventurous.

When we combine the super-symmetrical two dimensional power of the Hexagon with the transcendant, wandering but proportionally recursive irrationality of the Pentagon, we are taken into other dimensions of the Golden Ratio

In 1996, the Nobel Prize in Chemistry was awarded to three chemists for their discovery of a carbon molecule known as the "buckyball". The buckyball was named after the famed architect R.Buckminster Fuller whose unique structures called Geodesic Domes resembled soccer balls. [with acknowlegments to "The MATH and PHYSICS of soccer! - Page 1:"]
buckyball

Mathematically, the buckball (and the soccer ball) is an Archimedean Solid called a "truncated icosahedron" - a polygon with 60 vertices and 32 faces, 12 of which are pentagons (5-sided objects) and 20 of which are hexagons (6-sided objects).

In 1999, buckyballs were found trapped inside a 4.6-billion-year-old meteorite that landed in Mexico three decades ago and, recently, groups of buckyballs have been used to fight cancer.

APRIL 2nd 2006
Pentangles are used in many decorative designs
baringand also in my family crest,
a fact that has only just
dawned on me.

Let us move on from this now and see
if some ideas come out of the Fibonnacci
numbers that can make the design of the universe more natural
and less of a mystery. There are those who find any idea that logic lies
behind the wonders of creation and the glories of art and beauty as in some way
diminishing. I can't say I share this view. The unknown is always exciting and is to all intents endless, but invention means finding and dis-covery means just that.

Many people have tried to find a principle or theory behind nature. We see that there has been physical and chemical and biological evolution because while we experience the passage of time we are able to look back into the past. We have more than our personal memories and more than the collected memories of others in the form of written history. We can dig into the past on the surface of this planet. We can bore into trees, But even more remarkably we can look back an examine every stage of the evolution of the universe because due to its size and rate of expansion and the finite speed of light, the images and even the effects of the past are preserved in exemplar form. While any particular object can only be observed in the sate it was at the moment the information reaching us left it, we know that the elemental structural nature of the universe is the same in different places. So by choosing the distance of the observed object we can select the date. The same is true of drilling down to layers of strata or an ice-cap which has been built up by continual accretion on the surface.

Based on our examination of the history of the universe, the solar system, the planet earth, organic life and human life, various theories have been developed. Physicists search for a 'Theory of everything' that coordinates all the physical laws they know. Such a theory does not necessarily explain existence, just how existing energy and matter behaves and why. Biological evolution has seen the development theories of natural selection (incontestable) and of random mutation as the basis of the variations on which this selection acts. It is now accepted that while there may be random mutations there are also evolutionary trends and developments that are very far from random as the complexity of organisms prescribes the possibilities in some ways as it enlarges them in others. At the cutting edge, geometry and arithmetic decides the probabilities and, as we have seen in our brief examinations above, the mathematics are not as random as we might suppose.

There are many theories that can be set up as ways of looking at and explaining evolution at the organic biological level. The Selfish Gene theory of Richard Dawkins no doubt has something to tell us about one aspect of the survival techniques of species. But it is possible to propose many such theories, some reductionist, some holistic. They may not be mutually exclusive. Here is one I invented this morning based the Fibonacci sequence and the Golden Ratio. I have called it Predator Theory. I imagine it must have already been invented by others. All inventions are possibilities sitting there waiting to be expressed.

In Predator theory, we start with energy emanating from a singularity, and suppose a minimal pattern imposed on it in space-time, - an initial frequency, like a musical note, a 'word'. It has no meaning other than that as a result, space-time is no longer utterly bland . This corresponds with conventional thinking about the universe we observe, and we can call the energy 'dark energy' just as we do now for our universe. The pattern causes the universal expansive force which is otherwise infinitely entropic to cause relative compression in some places and this is the start of the gravitational effect, whereby, when matter is formed out the energy, it exaggerates the differential and very gradually the overall repulsive force causes a corresponding coalescent effect .

For our theory, we will ignore all of the physics and chemistry so far discovered, the business of matter and anti-matter, and stipulate only the possibility that any matter that comes into being then has the possibility to associate with any other matter brought within its reach, by any force or combination of forces that can act in the circumstances. We shall ignore all qualities and consider only quantities. We shall assume that initially matter is formed in units of ONE, whatever this matter may be e,g, quark, proton, neutron, electron, molecules, anything at all and will then associate according to what is available.

Units will first find other units, combining to form a combination with value 2. Those with value 2 will be most easily able to influence the dynamic trajectory of remaining adjacent units, becoming 3. Matter with value 3 will find and predate available 2s, making 5s. The nearest available meal for 5s will be the remaining 3s. In this way there will be a tendency to favour any assemblage by capture in a way that is statistically less than random. Now it is a long time before we get to the formation from gas clouds to the first stars, which overgrow and massively implode as their huge mass condenses into violent quasars and other beasts of the early universe. Every sort of excess is formed and self-destructs, perhaps returning first through time via black holes to the origin, then bursting out in clouds of dust containing the elements formed in their giant furnaces which will form the next generation of stars in the forming galaxies. But all through this process there will be a bias against randomization, a bias that depends on absolutely nothing except the building on what is there.

Abstraction is overruled as soon as real events take place, and in that reality the Fibonacci sequence will automatically be favoured, for the same reason that men climbed Mount Everest: because it is there! As soon as some units have combined, you have two types, the ones and the twos. These make 3s. 2s and 2s make 5s, 5s and 3s make 7s. As we get to complex substances and large volumes, the Golden Ratio will tend to feature. Where it does, there will be harmonies and resonances that will cause other values to harmonise trancendantly. So, when we arrive at a solar system where this is a dominant feature (see http://goldennumber.net/solarsys.htm ) it is not hard to reason that many of the attributes that make life possible on earth could be the result of  Phi resonance which, in the anti-entropic environment which systems subject to the reflexive attractive gravitational force provide, can assemble mutually supportive proportions and provide planets at appropriate distances from appropriate suns with appropriate moons.

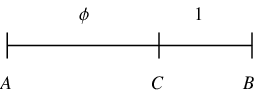
The Golden Mean then features in all life forms and as life develops to conscious and self-conscious minds we reach the point where we choose the proportions knowingly, as the basis of both practicality and beauty. Phi is the very means by which reductionist theories and holistic theories interact, for it demonstrates how the whole causes the parts just as much as the parts cause the whole, in any arrangement of nature.

APRIL 24th 2006
The previous paragraphs should help to explain to the reader why Oscar Wilde, though no mathematician, puts the following words into the mouth of Vivian in the Plato-istic dialogue "The decay of lying"

"The third doctrine is that Life imitates Art far more than Art imitates Life. This results not merely from Life's imitative instinct, but from the fact that the selfconscious aim of Life is to find expression, and that Art offers it certain beautiful forms through which it may realize that energy. It is a theory that has never been put forward before, but it is extremely fruitful, and throws an entirely new light upon the history of Art."

[Addendum Nov 2006]
I realise that at this point I should not have been tempted to move on to a discussion of Relativity, before finishing this section with a discussion of the Pentatonic scale in music. This scale is common to all cutures and is naturally 'hard-wired' into the human brain. 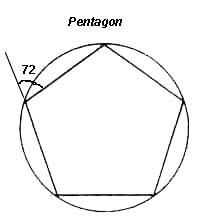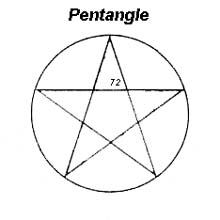Songs were written and performed using the notes of the pentatonic scale long before the different modes, intervals, scales and final merging of these in the 'equal temperament' compromise that permits all 'keys' to be used and all instruments to play together. The pentatonic scale, like the pentangel and pentagon, eixists as an apparently complete, finite presentation but, upon examination and use, forces us to explore the spaces and transcend.its limitations. There is no doubt a relationship between the self-forming properties of the Fibonnaci sequence and Golden Ratio, and the hard-wired pentatonic scale in the human brain.

MAY 22nd 2006     E=mc2
We will now move on to explaining some of the other mathematical theories that are never explained to the general public by either mathematicians or scientists. The reason they are not explained is that these worthy men and women do not understand them themselves. They understand how to use them and get results, but you will see from the following they do NOT know how to explain them. Here are some scientists trying to explain E=mc2 - Einstein's famous equation.When you have read their 'explanations' you will have gained a small amount of knowledge from one or two of them and no understanding whatsoever. But read it carefully. Then you can read the explanation from me.

NOVA | Einstein's Big Idea | E = mc2 Explained (text version) | PBS

OK, if you have read that, here is the proper explanation of E=mc2.

First we will define mass, which is the m in the equation. Mass is the property of matter which gives it inertia. That is the measure of the resistance of an observable object to acceleration.

Acceleration is the alteration of velocity (speed in a given direction). For an object at rest relative to an observer to acquire relative velocity by acceleration, a force has to act on it. When that has been applied, the object will have acquired energy. We call this energy, now represented by its motion, kinetic energy. It is measured therefore according to the velocity relative to an observer and the resistance it exhibited in changing its velocity (which we have defined as its mass). Velocity could be measured in metres per second. Acceleration (change of velocity could be measured in metres per second added per second, which we call metres per second squared [m/s2]. 

Now this kinetic energy is relative. The kinetic energy of a speeding bullet is very small compared to another bullet fired just before from the same automatic machine-gun, but very high compared to a stationary target. So the initial kinetic energy is proportional to an initial velocity of zero and its muzzle velocity before it starts to slow due to air friction.  The acceleration takes place over time in the barrel of the gun. If we assume for the sake of argument this is a uniform acceleration we can take the average speed, which is half the muzzle velocity,

You can see how confused modern students are by this page http://www.newton.dep.anl.gov/askasci/phy99/phy99032.htm

Newton and Leibnitz together settled on a formula of E=½mv2 [though this does not, I am told, appear in Principia Mathematica] as the way to calculate the kinetic energy of an object relative to an observer at relative rest with respect to the object before it was accelerated.

Now, when matter is released from its local inertial cage and scoots off as radiation, there is no acceleration over time as there is no longer a mass to accelerate. The change is total and instant into 100% kinetic energy. There is no average to be taken. We can dump the ½. We can just use the final velocity to give the value, as it is the start value as well and we know that electromagnetic radiation travels at the speed of light which we write as 'c'. You can therefore assume E=mc2 the moment you accept that mass can be converted into energy. It could not be otherwise.

The strange thing is that this was not worked out centuries ago. Any time you sit in from of a warm coal fire you are witnessing an electrical phenomenon in which some mass is converted into energy. Admittedly it is a small amount of mass. A lot of Oxygen has been added to the combustible material. But If you collect all the Carbon Dioxide and other gases and the ashes and clinker, you will find a small difference. But that's the point. It only needs a tiny amount and a coal fire does not give off radiation at wavelengths that damage us unless we are so close as to be burned. We are not dealing here with smashing the nuclei of atoms, releasing energy at wavelengths shorter than X-rays, just setting up a great game of musical chairs with the electrons till some of them can't sit down. We end up with elements that have less mass and less energy when at theoretical rest than the ones we started with.

Now of course not all the heat from a coal fire is radiation by the time it emerges. A lot of hot gas goes up the chimney but that is radiating as well. Nor is the radiant heat from the fire in the most part the direct result of matter being converted into energy, but the change in energy level of electrons which results from the chemical reactions in the fire. This cviolent hemical reaction causes the minute transfer via kinetic energy of charged particles (protons and electrons) which generate the electromagnetic waves of light and heat. Because there are billions of them, the overall effect is significant. Nevertheless, E=mc2 rules in the overall equation of a coal fire.

In due course, when I have moment, I will explain the paradoxes which you will have had to swallow in the explanation of the speed of light being the same for different observers even when they travel past each other at speed in the opposite direction. And I will explain what happens as you approach the speed of light which of course, according to that scenario, you could not do. Yes folks, the fact is your teachers do not understand it either or, when they do, cannot explain it properly. The same is true of religion, which is not understood by many Archbishops, Rabbis or Mullahs. They learned what they were taught. They learned how to make it work for them and the best make it work for others. In fact the same goes for all human knowledge that I have looked at so far. Some amazing brains have been employed producing amazing results, but they don't understand it really. As they get close to understanding these things they realise that there are problems in their world-view. Ask anyone developing quantum computing. If they are truthful...

Since writing the above I have listened to a news report triggered by the appearance in the sale room of some of Einstein's papers. The point is made that his big contribution was as a physicist and a visionary of the big picture rather than a mathematician. This is true. He took his maths from existing formulae developed by others. The 'squared' in c-squared was suggested by a woman whose name I forget many decades earlier and the formulae for General Relativity (which makes sense out of Special Relativity) come from a Frenchman in the 1700s whose name I have also forgotten - Eloi somebody. That in no way diminishes Einstein's work. There is a pile of maths knocking about looking for a home. It's a language developed from observation of Nature, just like English.  It can be fiction or realised in fact. We are often quoting Shakespeare to describe reality.

SUMMARY SO FAR:
If  in Newtonian physics E=½mv2 is true (which has been accepted for centuries)
  and
If  matter in any amount at all can be released or forced from its inertial bonds as radiant energy,
  then
It follows that E=mc2 must be true with or without any Theory of Relativity

MAY 24th 2006
Now that we have seen why the formula for the equivalence of mass and energy is indeed E=mc2, and that this is a Newtonian construct, we can have a look at Special Relativity. By using the symbol c for the speed of light we have avoided giving it a value. But clearly to get a numerical output from the formula, on the supposition that we have a value for the mass, we need to choose a value for c.

Here I am greatly relieved to find today that true understanding has permeated the international community and been set before the public now at no charge in Wikipedia. I don't know who wrote that page, but I am unspeakably grateful to them. I wish I had known them in 1983 when I was despairing of the failure of science journalism or textbooks to explain Einsteinian rather than Newtonian relativity. Happily, in 1983 a fundamental change was made to the system of SI Units (metres, seconds, grams etc.).  Before October 21st 1983 the speed of light was a measurement, arrived at by experiment, in metres per second. Since that date c has been accepted as a mathematical constant on which metres and seconds depend.

One metre is now defined as the distance light travels in a vacuum in 1/299,792,458 of a second. Only when this is accepted and understood can any discussion of Special Relativity make the slightest sense. [Note: There is a lot mre to Special Relativity than E=mc2, but later...]

The reason why it is not 1/300,000,000 of a second is that the metre had already been established, as had the second, in relation to other realities of global science and commerce. The metre was meant to be one ten-millionth of the distance from the equator to the north pole, which was then formalized in 1889 as the International Prototype Metre as the distance between two lines on a standard bar, kept in Sevres, of an alloy of ninety percent platinum and ten percent iridium, measured at the melting point of ice. In 1893 this distance was measured with an interferometer using light. Had we started with the current method of defining length in terms of the distance light travels in a time, we could have chosen 1/300,000,000 seconds as the time, but changing it now is too complex and would have repercussions.

But I digress. Although E=mc2 is, as I have emphasized, a Newtonian construct, it contains in c a function of electromagnetic waves, which we call (to keep it simple) light. Therefore it has to be reconciled with the formulae of James Clerk-Maxwell which describe the mathematics of electromagnetic phenomena. Newton and Clerk-Maxwell's formulae are irreconcilable in a context where time, distance and the speed of light are all constants regardless of the motion of objects and observers Something has to give! This is where Albert Einstein (a) appreciated the problem and (b) imagined the solution.

MAY 25th 2006
Now, before I go on, I just have to clear the decks with the professionals. Those who know me well understand that I have spent my life torn between exasperation with orthodox interpretations of the world and the 'cooking' professionals who are stuck with these, and admiration for those professionals whose mastery of their subject and control of their thinking is what has produced the miracles of technology and art that form the civilisation on which we all depend. It never occurred to me (silly, I know) to look up this subject in Wikipedia before starting on it. Having now done so I am deeply moved by the care taken on http://en.wikipedia.org/wiki/Mass to get to grips with the subject. I started off this file on Mathematics by deploring the failure of professionals and teachers to explain things even when they understood them, which often they did not. I have to admit that the guys writing this stuff in Wikipedia are really with it. However I am going to take issue with one important point. I am including here a couple of paragraphs from the page I have just refrenced. I am goig to take issue with the last sentence of each paragraph.

Wikipedia Extract:
For a macroscopic object, the rest energy mc2 includes the thermal energy, which depends on the temperature of the object, and is related to the random motion of the atoms or molecules of which the object is composed. This contribution is usually much smaller than the total rest energy, but often bigger than the kinetic energy. For example, if two objects stick together after a collision between them, the total kinetic energy of the objects is not conserved, and a significant part of it is transformed into thermal energy, so their mass increases by a tiny amount. Similarly, metabolism, fire and other exothermic chemical processes convert mass to energy, however the mass change is usually negligible.

My comment: small it may be, negligeable it is not.  Ignoring it is why E=mc2 was thought to be something new, to do with Relativity and Atomic Bombs, instead of Newtonian logic. It is only when we decide that c is a constant that Relativity raises its head, and nuclear fission does not prove Relativity.

Wikipedia extract:
More significant changes of the rest energy occur in processes that split or combine subatomic particles. The reason is that mass, as we have defined it, is not conserved during such processes. The simplest example is the process of electron-positron annihilation, in which an electron and a positron annihilate each other to produce a pair of photons: the electron and positron both have non-zero mass, but the photons are massless. Other examples include nuclear fusion and nuclear fission. Energy, unlike mass, is always conserved in special relativity, so, roughly speaking, what is happening in these reactions is that the rest energy of the reactants is being transformed into the kinetic energy of the reaction products. The fact that rest energy can be liberated in this way is one of the most important predictions of special relativity.

My comment:  I do not see Special Relativity as predicting that energy can be liberated in this way. Energy always was and is liberated in this way. The formula is inevitable, as I have shown. Special Relativity deals with the theoretical problems that arise as a consequence of understanding this and in certain practical applications involving extremes of accuracy, velocity and distance measurement.

Another point I wish to make at this stage is that the definition of mass that I used at the start [May 22nd] is the definition of Inertial Mass. Wikipedia has very correctly stated that there are definitions of Gravitational Mass (active and passive), and that no experiment has ever detected a difference - which leads us to General Relativity later. However, for the moment the definition I have used is what I meant to use.

Finally (for today) I want to take the opportunity to note that  while Donald G. Shead 54 Chaplin St, Chaplin CT 06235 suggested a definition of MASS as:
(a) "the mutual resistance of two particles, bodies or masses of material matter from simultaneously occupying and/ or passing throught the exact same place" and/or (b) "the mutual resistance of the penetration of a body resting on a planet's terra firma surface." - that is a definition of MATTER, and quite a good one. The (a) option has always been the one I favoured. It is not (for me) a definition of MASS, as opposed to MATTER, even though there may be circumstances when one implies or infers the other.

JUNE 28th 2006
I am sorry about the delay in completing the explanation of Special Relativity and General Relativity but I have to be in the mood in order to hit the spot and clear up the misunderstandings. It is no good just spouting stuff. Today's double page spread in The Independent has some attempted explanations of Gravity Waves but does not really give the right picture. It does not help that they are wrongly named - they should be called INERTIAL WAVES, but Einstein was trying to keep it simple knowing most people had heard of gravity.

MARCH 17th 2007
Before getting back to General Relativity it is time to pay tribute to a programme trilogy on UK BBC 2 called The Trap. The fundamental issue examined in The Trap concerns the need to advance from the basic Game-Theory of John Nash and the Selfish-Gene theories of Dawkins and others.  Nash is alive and well and in a state of enlightenment, realising his theory is (a) inadequate in relation to the complex human beings it aims to include in its behavioural models and (b) subject to the universal law of all theories of this kind: they contain the seeds of their own destruction which will germinate if application is taken close the extreme. Dawkins, although he still fails to understand his selfish gene theory has no effect whatsoever on arguments for or against atheism, has learned a lot more than he knew when he first got so excited about it. It's extraordinary how people burst into print and lecturing before finding out what othrs have already discovered many times over the past few thousand years, but there you go..

The Trap is not without a few misperceptions of its own. In its effort to show that the chasing of numerical targets by hospital managers, targets set according to game-theory rules to incentivise those responsible, it found fault with classifying a trolley with wheels removed as a bed, or a corridor converetd ito a ward as a ward. Why? A bed is a trolley without wheels and a large corridor full of beds is a ward. If beds and wards were needed, that was how to add them quickly and speed was what was requested. In fact the NHS invested far too much as it is, which is why it spent locally beyond its means and s now introuble because of that. Putting off complicated operations to get the quick ones off the waiting list may or may not be cheating with harmful side effects but more detail needs to be shown to establish that. Nevertheless on the whole The Trap is intelligent and thought provoking.

MARCH 25th 2007
Well that was easy. The third episode of The Trap finished with an indicated conclusion: that Isaiah Berlin was wrong when he said that liberty had to be limited to what he defined as 'Negative Liberty' (because, if it were given a collective aim or vision, this would end as tyranny). If that is indeed the conclusion of the author I can confirm without doubt that this conclusion is correct, and that a philosophy of liberty such as Berlin's, necessary and valid as it was to enable us to defeat that of Marx, is nevertheless useless as a formula for existence, just as was the mathematical basis for it proposed by Nash.

So what, you may ask, is the positive aim that we should encourage the world's citizens to strive for in both their own and the collective interest, not because they are forced to but willingly?.Very simple: it is the one that Nature shows us - the management of this planet. That means managing our immediate personal environment and relationships, our local and our global environment and relationships. By facing us with a crisis, Nature has supplied us with the answer. Now that we know that the negative freedom of Isaiah Berlin or the Positive Freedom of Marx will both lead to disaster, we can perhaps begin to see that we can serve ourselves best by serving others.  Neither formulae from Nash or Philosophy from Berlin or Marx can obsolve us each and every one from our personal responsiblity. That is to inform ourselves and educate our children. We have millennia of works to choose from, so I suggest a sensible way to proceed is to look first at what informed some of those whose lives we most admire. A lot of stuff is free on the web and we have an Open University and the Bible (Auhorized version) and Shakespeare, and all the works of philosophy and science; but first of all we much teach people to listen, speak, read and write in at leat one or two established modern languages. English is a good one.

APRIL 17th
Getting back into Special and General Reativity, I am pasting here an important news item which I will use to deal with Einstein's Relativity in due course. It concerns what we call 'the fabric of space-time' and its interaction with concentrations of energy (such as significant mass).

Einstein was right, probe shows
Early results from a Nasa mission designed to test two key predictions of Albert Einstein show the great man was right about at least one of them.

It will take another eight months to determine whether he got the other correct say scientists analysing data from Nasa's Gravity Probe B satellite.

The spacecraft was launched into orbit from California, US, on 20 April 2004.

The mission's chief scientist presented details at a physics meeting in Jacksonville, Florida.

Gravity Probe B uses four ultra-precise gyroscopes to measure two effects of Einstein's general relativity theory.


A scientist starts with a bulldozer, follows with a shovel, and then finally uses dental picks and toothbrushes to clear the dust away from the treasure. We are passing out the toothbrushes now
William Bencze,
Stanford University

One of these effects is called the geodetic effect, the other is called frame dragging. A common analogy is that of placing a heavy bowling ball on to a rubber sheet.

The bowling ball will sit in a dip, distorting the rubber sheet around itself in much the way a massive object such as the Earth distorts space and time around itself.

Minute measurements

In the analogy, the geodetic effect is similar to the shape of the dip created when the ball is placed on to the rubber sheet.

If the bowling ball is then rotated, it will start to drag the rubber sheet around with it. In a similar way, the Earth drags local space and time around with it - ever so slightly - as it rotates.

Over the course of a year, these effects would cause the angle of spin of the gyroscopes to shift by minute amounts.

The mission's principal investigator, Professor Francis Everitt, from Stanford University, discussed preliminary results at the American Physical Society meeting in Jacksonville at the weekend.

The data from Gravity Probe B's gyroscopes clearly confirm Einstein's geodetic effect to a precision of better than 1%.

The scientists from Stanford are still trying to extract its signature of frame-dragging from the data.

They plan to announce the final results of the experiment in December 2007, following eight more months of data analysis.

Larger puzzle

Professor Tim Sumner, a physicist at Imperial College London, told BBC News: "Having an announcement at this stage, on the way to the final result, is very encouraging. I'm very pleased to see that the result has now been released.


There is an expectation that at some level we will expose a departure from pure general relativity as envisaged by Einstein
Professor Tim Sumner,
Imperial College London

"Most individual measurements are part of a larger puzzle. But general relativity is one of the big branches of physics and it is poorly tested at the moment because of the relative weakness of gravity as a force."

"I would see this as a piece of solid verification to underpin general relativity, which occupies a special place in physics."

William Bencze, Gravity Probe B programme manager at Stanford University in California, said: "Understanding the details of this science data is a bit like an archaeological dig.

"A scientist starts with a bulldozer, follows with a shovel, and then finally uses dental picks and toothbrushes to clear the dust away from the treasure. We are passing out the toothbrushes now."

Unified theory

Tim Sumner said few physicists were expecting to see a deviation from Albert Einstein's predictions in this experiment.

But he said that other tests could start to reveal cracks in general relativity, suggesting where modifications might be made.

Physicists have been unable to incorporate gravity into a unified theory to describe all that is known about the fundamental forces between elementary particles in nature.

Modifications to general relativity could be important steps towards a unified theory.

"There is an expectation that at some level we will expose a departure from pure general relativity as envisaged by Einstein," Professor Sumner said.

"One of the areas of general relativity that is less well founded is when you get into very intense gravitational field interactions. Some astrophysical objects will be in very high field situations such as pairs of massive black holes orbiting one another."

A joint mission between Nasa and the European Space Agency called Lisa (Laser Interferometer Space Antenna) will study gravitational waves coming from binary systems such as these.

General relativity is not expected to break down in these situations. But Lisa should help scientists understand how the theory works in "high field" gravitational regimes such as pairs of massive black holes.

Other experiments are due to test the equivalence principle, one of the foundation stones of general relativity. This principle stems from the observation that when two objects are dropped, they will accelerate at the same rate.

"Here there is a theoretical framework where one might expect to see a departure from the equivalence principle," said Professor Sumner. "This might give us pointers as to the way forward."

The Imperial College physicist is involved in two mission concepts to test the equivalence principle. One is the Satellite Test of the Equivalence Principle (Step), which has been proposed by some of the same scientists involved in the Gravity Probe B mission. Another is the GrAnd Unification and Gravity Explorer (Gauge).

Gravity Probe B was launched from Vandenburg Air Force Base in California on 20 April 2004. It transmitted its data for exactly 50 weeks, from August 2004 to August 2005.

Story from BBC NEWS:
http://news.bbc.co.uk/go/pr/fr/-/1/hi/sci/tech/6561391.stm

Published: 2007/04/16 18:16:20 GMT

© BBC MMVII

APRIL 19th 2007

Melvyn Brag to the rescue. I was searching for a new way into Special and General Relativity and realise the best is the old way - to call on some of the the history of mathematics in the domain of symmetry. We have looked at some of this by accident on the way already but this morning it got beautifully kicked around on In Our Time on Radio 4. Symmetry theory has been our guide to exploring local reality, telling us where to look. Paradoxically, the breaking of symmetry as we theoretically approach extremes of scale in space and tine is the only way our dynamic existence could...er... exist. By all means listen to this broadcast next. Don't dispair though if you don't understand it or understand only bits of it. We only need to pluck a few points out.

Programme detail     IN OUR TIME

  Thursday 19 April 2007         http://www.bbc.co.uk/radio4/history/inourtime/inourtime.shtml                                                                       
Symmetry
SYMMETRY

Today we will be discussing symmetry, from the most perfect forms in nature, like the snowflake and the butterfly, to our perceptions of beauty in the human face. There's symmetry too in most of the laws that govern our physical world.

The Greek philosopher Aristotle described symmetry as one of the greatest forms of beauty to be found in the mathematical sciences, while the French poet Paul Valery went further, declaring; “The universe is built on a plan, the profound symmetry of which is somehow present in the inner structure of our intellect”.

The story of symmetry tracks an extraordinary shift from its role as an aesthetic model - found in the tiles in the Alhambra and Bach's compositions - to becoming a key tool to understanding how the physical world works. It provides a major breakthrough in mathematics with the development of group theory in the 19th century. And it is the unexpected breakdown of symmetry at sub-atomic level that is so tantalising for contemporary quantum physicists.

So why is symmetry so prevalent and appealing in both art and nature? How does symmetry enable us to grapple with monstrous numbers? And how might symmetry contribute to the elusive Theory of Everything?

Contributors

Fay Dowker, Reader in Theoretical Physics at Imperial College, London

Marcus du Sautoy, Professor of Mathematics at the University of Oxford

Ian Stewart, Professor of Mathematics at the University of Warwick


Discussion to follow soon

JANUARY 15th 2010
OK, I had to wait for something to trigger a better debate and here it is Jim Al-Khalili comes up with a decent compendium of ideas on BBC TV

The Secret Life of Chaos

Documentary in which Professor Jim Al-Khalili shows how chaos theory can answer a question that mankind has asked for millennia - how does a universe that starts off as dust end up with intelligent life? It's a mindbending, counterintuitive and for many people a troubling idea.

It's not a troubling idea at all. It's not even counterintuitive. Come to think of it I should have moved on to add the Mandelbrot work to enlarge on my point that given the basic geometry of space-time and gravitation, chaos theory allows the opposite of chaos to 'self-organise'. That has been the burden of the argument that follows from the parallel inevitable self creation of the Fibonnaci sequence and consequence of Phi. Order and Chaos are indeed linked as Al-Khalili indicates, but the idea is not nearly as revolutionary is he pretends. It could hardly be otherwise. Nor does it have any bearing on the existence or not of "God", other than to remove the need for the interventionist God-the-mechanic hovering with an oil-can and interfering with faulty designs. Evolution is a fact compatible with the simple and beautiful statement of St John; "in the beginning was the Word, the word was with God and the Word was God........and the Word became Flesh. This is one more step in our understanding how. Of course the first trick, not covered by Al-Khalili, was the emergence from singularity, into space-time with universal gravitation and mass-energy equivalence, when all the dice there ever can be were mathematically thrown so as to literally self-organise and mutually select according to the laws of we are now getting to grips with. In trying to summarise The Secret Life of Chaos in a single sentence the headline writer has in fact misled the reader. Chaos Theory does not 'answer' the problem at all, but a better understanding of Chaos Theory shows that it allows, by the freedom freedom it permits, Nature to construct the ever-enhancing means of experience that time will test, sometimes to destruction that in turn allows creative evolution at the 'coal-face' of existence.

We can go further. While these mathematics give us means of understanding how the future can be uncertain, and how we as part of nature can be freed from determinism, there are rules of harmony that can profitably exploited. The forces of evolution can be understood and exploited. Just as in the case in quantum theory, there is in the chaos of self-organisation the equivqlent in aggregate systems of a 'back-EMF' of interaction, due to the presence of the surrounding environment. We cannot tell which pattern will be produced but we can tell what kind of pattern given certain parameters, borders and seeds etc. The points were well made by Al-Khalili, my objections are only to the hype. There was also a strange political angle introduced in connection with the unfortunate Alan Turing, and early proponent of some primitive self-organisation theories.

Turing was disgracefully treated for reasons curiously beyond the control of the authorities at the time. Homosexuality being a crime at the period he lived, he was subject to threats of blackmail. Since he was the single person in possession of most government secrets, this created an impossible situation on paper. He agreed to be treated medically to remove his sexual feelings. The result led him to suicide. I could not see it's relevance to the programme, however. The man was a genius, but there are many more obvious approaches to self-organisation than Turing's that lead far further.

In conclusion: great stuff Jim, but what took you professional scientists so long.

nnnn